在數學中, 一個n實數的序列可以被理解為n維空間中的一個位置。當n等於七時, 所有這樣的位置的集合被稱為 七維空間。 通常這種空間被研究為一個向量空間,而沒有任何距離的概念。 七維歐幾里得空間是一個配備了一個歐幾里得距離的七維空間,它由點積定義。
更廣義的來說, 該術語可以指任何體 (數學)上的七維向量空間,例如七維複矢量空間,其實際有著十四個維度。 它同時也可能指七維流形例如七維球面,或其它各種幾何構造。
七維空間有許多特殊的屬性,其中許多與八元數有關。 一個特別獨特的屬性是向量積僅可以在三維或七維中定義。 這些皆和胡爾維茲定理相關,它禁止像四元數以及八元數這樣的代數結構在除了1,2,4和8之外的維度的存在。 第一個被發現的異構球體是七維的。
概述
根據90年代提出的M理論(超弦理論的一種),宇宙是十一維的,由震動的平面構成的。在愛因斯坦那裡,宇宙只是四維的(三維空間和一維時間),現代物理學則認為還有七維空間我們看不見。 科學家們對我們已認知的維與可能存在但未被認知的維之間的區別是如何解釋的呢?他們打了一個比方:一隻螞蟻在一張紙上行走,它只能向右或向左,向前或向後走。對它來說高與低均無意義,這就是說,第3維的空間是存在的,但沒有被螞蟻所認識。同樣,我們的世界是由四維構成的(三個空間維,一個時間維),但我們沒有覺察到所有其他的維。
幾何學中
七維多胞形
在七維空間中的多胞形都稱為七維多胞形。 最常見的是正多胞形,而這些正多胞形在七維空間中只有三個: 七維單純形,七維超方形,七維正軸形。 而更廣義的類型是七維均勻多胞形,是由反射的基本對稱群構造出的,每一個域由考斯特群定義。 每一個均勻多胞形是由一個環形考斯特圖定義的。 七維半超方形是一個D7家族中的一個特殊多胞形,而321,231,以及132則是屬於E7系列。
| A6 | B7 | D7 | E7 | |||
|---|---|---|---|---|---|---|
 七維單純形 |
 七維超方形 |
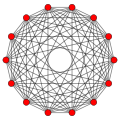 七維正軸形 |
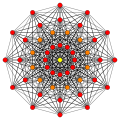 七維半超方形 |
 321 |
 231 |
 132 |
六維球面
六維球面,或是七維空間的超球體, 是一個從六維曲面到中心點皆等距的超球體。它的符號為S6,而關於六維球面的方程式,設半徑為r,其超球心為
而這個六維球面在七維空間的體積是
也就是4.74277 × r7,而一個七維超立方體中最大的內接七維超球大約等同於該七維超立方體的0.0369倍。
應用
向量積
七維向量的向量積,是一個向量值,是七維空間中兩個向量的正交乘積,其具有雙線性、反交換的性質。與三維中更常見的向量積不同,因為它不是一個可以簡單地被算出來的積。
七維空間是除了三維空間之外,唯一一個可以定義向量叉積的空間。[查证请求]
異構球體
在1956年,約翰·米爾諾構造出了一個在七維空間中的異構球體並且顯示在七維球面上存在至少七個可分辨的結構。 在1963年他表明這種結構的確切數目是28種。
參見
參考資料
- H.S.M. Coxeter: Regular Polytopes. Dover, 1973
- J.W. Milnor: On manifolds homeomorphic to the 7-sphere. Annals of Mathematics 64, 1956
外部連結
- Hazewinkel, Michiel (编), Euclidean geometry, 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4












