此條目介紹的是電動機的控制技術。关于火箭發射的推力控制技術，请见「推力向量」。

向量控制（vector control）也稱為磁場導向控制（field-oriented control，簡稱FOC），是一種利用變頻器（VFD）控制三相交流馬達的技術，利用調整變頻器的輸出頻率、輸出電壓的大小及角度，來控制馬達的輸出^[1][2]。其特性是可以個別控制馬達的磁場及轉矩，類似他激式直流馬達的特性。由於處理時會將三相輸出電流及電壓以向量來表示，因此稱為向量控制。

向量控制可以適用在交流感應馬達及直流無刷馬達^[3]，早期開發的目的為了高性能的馬達應用，可以在整個頻率範圍內運轉、馬達零速時可以輸出額定轉矩、且可以快速的加減速。不過相較於直流馬達，向量控制可配合交流馬達使用，馬達體積小，成本及能耗都較低，因此開始受到產業界的關注。向量控制除了用在高性能的馬達應用場合外，也已用在一些家電的應用中^[4]。

达姆施塔特工业大学的K. Hasse及西門子公司的F. Blaschke分別在1968年及1970年代初期提出向量控制的概念。Hasse提出的是間接向量控制，Blaschke提出的是直接向量控制^[2][5]。布伦瑞克工业大学的維爾納·萊昂哈德（Werner Leonhard）進一步開發磁場導向控制的控術，因此交流馬達驅動器開始有機會取代直流馬達驅動器。

當時微處理器尚未商品化，但已經出現泛用的交流馬達驅動器^{[6][7][4]:p.605}。當時相較於直流馬達驅動器，交流馬達驅動器的成本高、架構複雜，而且不易維護．而當時的向量控制需要許多感測器及放大器等元件，因此無法將向量控制應用在交流馬達驅動器中^[8]。

派克變換一直被用在同步馬達及感應馬達的分析及研究，是了解磁場導向控制最需要知道的概念。這個概念是羅伯特·H·帕克（英语：Robert H. Park）在1929年的論文中提出的^[9]。派克變換被列為二十世紀發表電力電子相關論文中，第二重要的論文。派克變換的重要性是可以將馬達有關的微分方程，由變係數微分方程變成「非時變」係數的微分方程^[10]。

利用向量控制，可以用類似控制他激直流馬達的方式控制交流感應馬達及同步馬達^[11]。在他激直流馬達中，磁場電流及電樞電流可獨立控制，在向量控制，控制磁場及電樞的電流互相垂直，理論上不會互相影響，因此當控制轉矩時，不會影響產生磁場的磁链，因此可以有快速的轉矩響應。

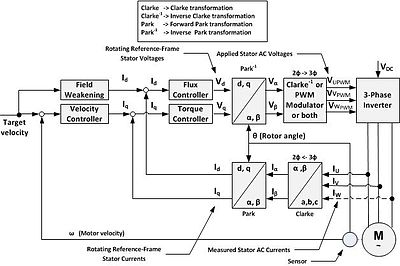
向量控制會依照程式中計算的電流向量，產生三相PWM的電壓提供給馬達，目的是要控制馬達的三相電流。其中會將電流及電壓等物理量在二個系統之間轉換，一個是隨速度及時間改變的三相系統，另一個則是二軸非線變的旋轉坐標系統^[12]。

定子電流的向量可以用（d,q）軸的坐標系統來定義，其中場磁链的電流分量對正d軸（direct），而轉矩的電流分量對正q軸（quadrature）。^[11]馬達的（d,q）軸坐標可以對應（a,b,c）三相的弦波系統。而（d,q）軸的電流向量一般可以個別用PI控制器進行控制，也就是沒有微分（D）單元的PID控制器。

和（d,q）軸的坐標系統有關的坐標轉換如下^[12][14][15]：

• 由三相的瞬時電流值轉換為（a,b,c）三相的弦波電流向量。
• 利用克拉克轉換，由（a,b,c）三相轉換到（${\displaystyle \alpha }$,${\displaystyle \beta }$）二相的轉換。在實現向量控制時一般假設馬達沒有接地，且三相電流平衡，因此可以只感測三相電流中的二相。（${\displaystyle \alpha }$,${\displaystyle \beta }$）二相的坐標互相垂直，${\displaystyle \alpha }$軸對齊（a,b,c）三相中的a相。將（${\displaystyle \alpha }$,${\displaystyle \beta }$）二相轉換到（a,b,c）三相的轉換則會利用空間向量PWM或是反克拉克轉換來達成。
• 在（${\displaystyle \alpha }$,${\displaystyle \beta }$）和（d,q）之間，二個二相系統之間的轉換，利用派克轉換及反派克轉換來達成。

不過也有些系統會直接進行（a,b,c）三相系統及（d,q）軸坐標系統之間的轉換及反轉換。

（d,q）軸的坐標系統可以依任何轉速旋轉，在實務上可以選擇以下三種不同轉速的坐標系統：^[13]

• 靜止坐標系統，（d,q）軸不會旋轉。
• 同步坐標系統，（d,q）軸以同步轉速旋轉。
• 轉子坐標系統，（d,q）軸以轉子的轉速旋轉，感應馬達的轉子轉速會和同步轉速不同。

利用馬達控制的演算法，可以從三相的瞬時電流中得到獨立的轉矩電流及場電流^[16]。簡單的交流馬達控制可以利用以微處理器為基礎的控制系統來達成^[16]．高階的交流變頻器則會應用数字信号处理器（DSP）來進行^[17]。

向量控制可以用有編碼器回授轉速的閉迴路磁場導向控制來實現，也可以用無（速度）感測器（sensorless）的開迴路控制器來實現。無感測器向量控制和閉迴路控制器的最大差異是可以輸出額定轉矩的最小速度。閉迴路向量控制可以在馬達靜止時輸出額定轉矩，而無感測器向量控制一般有其最小速度的限制，例如0.8Hz^[19]。

無感測器向量控制是利用三相電壓及輸出電流，配合開迴路的估測器（estimator）或是閉迴路的觀測器（observer）來得到轉速的資訊，開迴路估測器中會計算轉速，但不會作回授控制，閉迴路觀測器則會計算轉速，並依此計算某物理量，利用此計算量計算值和向量控制中對應值的差異進行回授控制。無感測器向量控制由於不需要有加裝編碼器的馬達，在成本及可靠度上很有競爭力^[15][18]，但對於電流信號的要求也比較高。

磁場導向控制可分為二種：分別是直接磁場導向控制（DFOC，也稱為回饋磁場導向控制）及間接磁場導向控制（IFOC，也稱為前饋磁場導向控制）。間接磁場導向控制可以在從零速到高於馬達額定頻率以上的弱磁區運作，因此較常使用^[23]。

直接磁場導向控制中，利用電壓型或電流型的磁通模型計算磁通大小及角度。在間接磁場導向控制中會先量測定子電流及轉子速度，再利用轉子速度及轉差率的計算值推導轉子角度，再得到磁通的角度^[24][25]。

• 需要量測（或是估測）馬達的速度或位置，若估測馬達的速度，需要馬達電阻及電感等參數，若可能要配合多種不同的馬達使用，需要自動調適（autotuning）程序來量測馬達參數。
• 藉由調整控制的目標值，轉矩及磁通可以快速變化，一般可以在5-10毫秒內完成。
• 若只使用PI控制，步階響應會有过冲。
• 功率半導體的切換頻率（載波）一般為定值。
• 轉矩的精確度和控制系統中使用的馬達參數有關，因此若因為馬達溫度變化．造成轉子電阻阻值提高．會造成誤差的變大。
• 對處理器效能的要求較高，至少每一毫秒需執行一次馬達控制的演算法。

變頻器除了使用向量控制外，另一種常用的技術是純量型的V/f控制，事先建好不同頻率下對應電壓的數據，變頻器的輸出電壓則依當時頻率查表（V/f曲線）而得。相較於V/f控制，向量控制需要有馬達電流、實際轉速等信號，架構較複雜，但控制性能也較V/f控制要好。

直接轉矩控制是另一種馬達控制的技術。相較於直接轉矩控制，向量控制的架構較要複雜，但其計算不需那麼頻繁，而且對電流感測器的要求也比較低。向量控制在處理器及週邊電路的成本較低，比較適用在一些不需要用到直接轉矩控制高性能的應用場合，