建議将此條目或章節併入连续函数。（討論）

此條目没有列出任何参考或来源。 (2015年9月23日) 維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。

在拓撲學和數學的相關領域裡，連續函數是指在拓撲空間之間的一種態射。直觀上來說，其為一個函數f，其中每一群在f(x)附近的點都會含有在x附近的一群點之值。對一個一般的拓撲空間來說，這是指f(x)的鄰域總會包含著x之鄰域的值。

在一個度量空間(如實數)裡，這是指在f(x)一定距離內的點總會包含著在x某些距離內的所有點。

因為有若干個對拓撲結構的等價定義存在，所以亦存在若干種定義連續函數的方法。

拓撲中最常見的連續概念之定義為將其定義為一個其開集之前像亦為開集的函數。類似開集的公式化，亦有一閉集公式化，其將連續函數定義為其閉集之前像亦為閉集的函數。

以前像為基底之定義時常很難直接地被使用。替代地，設有一由X至Y的函數f，其中的X和Y都是拓撲空間。則f會被稱為是在x為連續的，其中x為X的元素，若對於任一f(x)的鄰域V，都存在一個能使${\displaystyle f(U)\subseteq V}$之x的鄰域U。雖然此一定義看起來很複雜，其在直覺上是指不論V變得多「小」，總會可以找到一個包含可映射至V內之x的U。若f在X內的每一個元素x都會連續，則簡稱f是連續的。

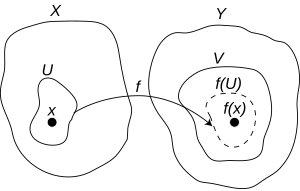
在一度量空間內，則其會等價於將所有鄰域替換成考量以x和f(x)為中心之開球的邻域系统。這會導致在實分析中對連續函數的標準定義，其敘述著一個函數若為連續時，則其靠近x的所有點都會映射至靠近f(x)的點上。這只在度量空間中有意義，因為只有在度量空間中有距離的概念。

在一些文章中，空間的拓撲會被簡便地以極限點來描述。